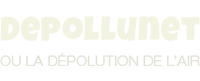2.3. Les pressions mises en jeu en aéraulique
Dans les installations d'aspiration le déplacement de l'air se traduit par des frottements qui s'exercent sur les conduites avec plus ou moins de forces suivant la nature plus ou moins grossière de la surface intérieure des parois. Ces frottements s'effectuent naturellement beaucoup plus fortement lorsque les conduites présentent des coudes, des rétrécissements, des élargissements ou des convergences.
C'est l'ensemble des pressions dynamiques et statiques d'un réseau qui déterminera la consommation électrique à prévoir au ventilateur.
2.3.1. Pression dynamique Hd
Une pression dynamique donnée correspond à la force requise pour accélérer la masse d'un fluide depuis l'état de repos jusqu'à une vitesse donnée ; elle est égale à la force qui s'opposant à l'écoulement, serait capable d'immobiliser la masse du fluide en mouvement ; elle ne s'exerce que dans la direction de l'écoulement du fluide.
La pression dynamique est aussi nommée pression cinétique.
En unité légale (système SI), la pression P est exprimée en pascal (Pa) et a l'expression :
P = g h
ou P = masse volumique de l'air en kg/m3 (à 15°c sous une pression normale 1,013 bar ou 760 mm de mercure, = 1,226 kg/m3)
g = accélération de la pesanteur en m/s2 (g= 9,81 m/s2)
h = hauteur de la colonne d'air en m
P = 1,226 x 9,81 x h
Pendant plusieurs années, et pour des raisons pratiques en aéraulique, l'habitude est d'exprimer les pressions non pas en pascal (unité légale SI) mais en millimètre de colonne d'eau (mm CE) qui est la valeur lue directement sur les appareils de mesure utilisés (voir note ci-dessous). Si Hde est la hauteur lue en mm CE, la pression P en pascal aura pour expression :
![]()
r' étant la masse volumique de l'eau = 1000 kg/m3
![]()
Soit 1 mm CE = 9,81 Pa ou 1 Pa = 0,102 mm Ce
D'une manière générale 1 mm CE 10 Pa ou 1 daPa
En égalant les deux expressions et de la pression, il vient :
![]() ou
ou ![]() soit
soit ![]()
D'où on tire : ![]()
force vive = énergie cinétique
La vitesse initiale étant nulle, la force vive initiale l'est aussi, et la variation de force vive totale de la particule de densité est donc égale à :
![]()
La force ayant agi pendant le même temps sur la particule est la force de la pesanteur ;
En portant la valeur dans l'expression précédente, elle devient :
![]()
Formules à retenir :
![]()
2.3.2. Pression statique Hs
Nous avons vu précédemment que tout obstacle placé sur le chemin des filets d'air exerce sur ceux-ci une action de freinage qui se traduit par une chute de la vitesse de l'air.
Par conséquent, si on désire un maintien de la vitesse de l'air malgré les obstacles existants, il faut fournir un effort supplémentaire en donnant au fluide un surcroît d'énergie destiné à vaincre les forces de frottement.
Cette pression complémentaire exercée sur le fluide, sous un certain débit est appelée Pression Statique. Elle s'exerce dans toutes les directions.
La pression statique se mesure perpendiculairement à la direction du mouvement de l'air (voir Figure 6).
Figure 6
Mesure de la pression statique
Selon la position de la mesure (refoulement ou aspiration) la pression statique peut être soit supérieure, soit inférieure à la pression atmosphérique.
2.3.3. Pression totale Ht
On appelle pression totale existant dans une conduite aéraulique la somme des deux pressions dynamiques et statiques (la pression totale est parfois aussi nommée pression d'arrêt).
La pression totale Ht est donc la somme algébrique des pressions statique et dynamique:
![]()
La valeur de la pression totale est significative du choix du ventilateur. Dans des conditions d'emploi bien définies, un ventilateur est générateur d'une pression totale constante.
Les différents termes peuvent être mesurés séparément à l'aide d'un tube PITOT (du nom de son inventeur voir Figure 10)
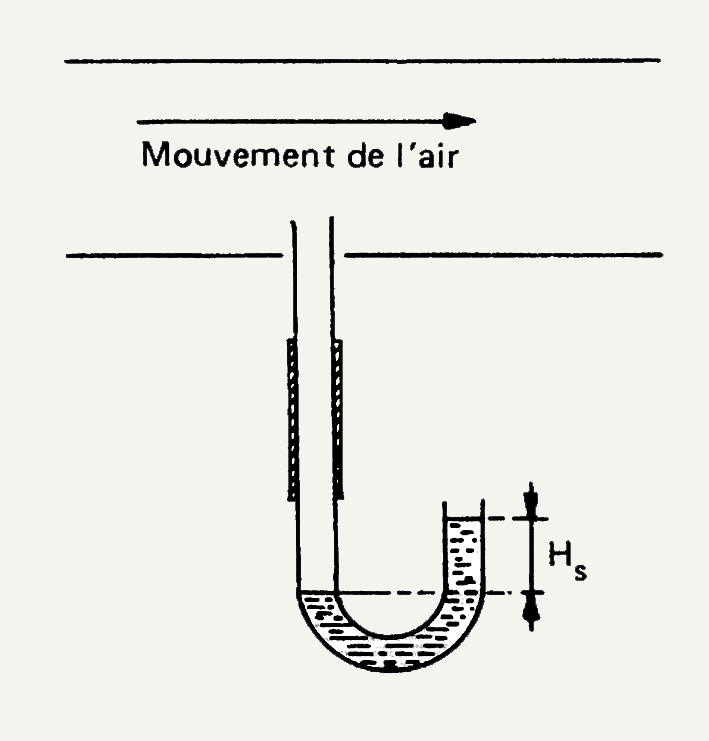
Figure 7 :
Pression statique, totale et dynamique (cas en dépression)
2.3.4. Relation entre les pertes de charge et la pression dynamique
Nous avons vu que l'air s'écoulant entre deux sections d'une canalisation subit une chute de pression totale p (Pa) appelée perte de charge. Les pertes de charge représentent l'énergie dégagée sous forme de chaleur dans l'unité de volume sous l'effet des frottements dûs à la viscosité de l'air ; elles sont liées à la vitesse de l'écoulement et donc à la pression dynamique.
De nombreuses études aérauliques ont été entreprises afin de déterminer une relation simple entre la perte de charge statique et les diverses caractéristiques du fluide et des tuyauteries composant un circuit d'aspiration.
L'Anglais REYNOLDS mit en évidence l'existence d'un facteur sans dimension appelé nombre de REYNOLDS dont la valeur est significative de l'ensemble aéraulique considéré (fluide et circuit de transport).
La perte de charge (exprimée en Pascal) significative d'une conduite cylindrique peut s'exprimer alors par la formule suivante:
![]()
ou
HS = ß ( l / d ) V² / 16,
l, d longueur et diamètre du conduit (m),
ß coefficient de friction lié au nombre de Reynolds,
V vitesse du fluide (m/s).
Pour de la gaine d'acier lisse ce coefficient est environ de :
ß = 0,025 l / d pour 80 < d < 125 mm
ß = 0,022 l / d pour 125 < d < 225 mm
ß = 0,020 l / d pour d > 225 mm
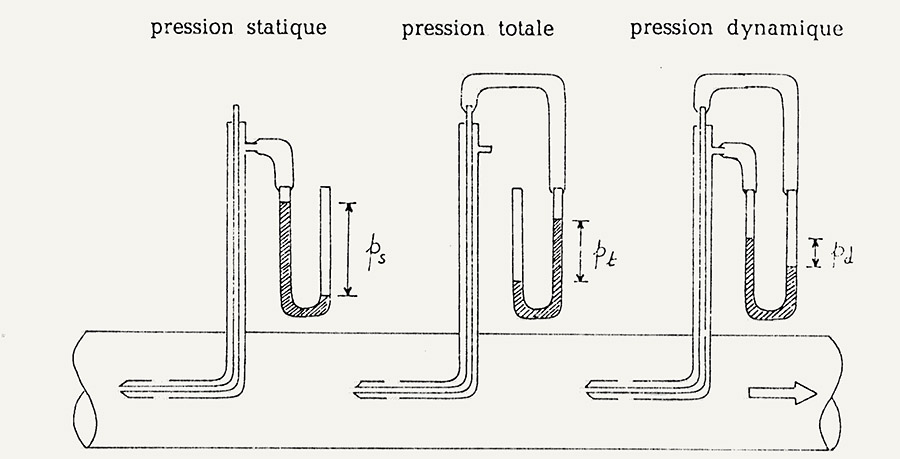
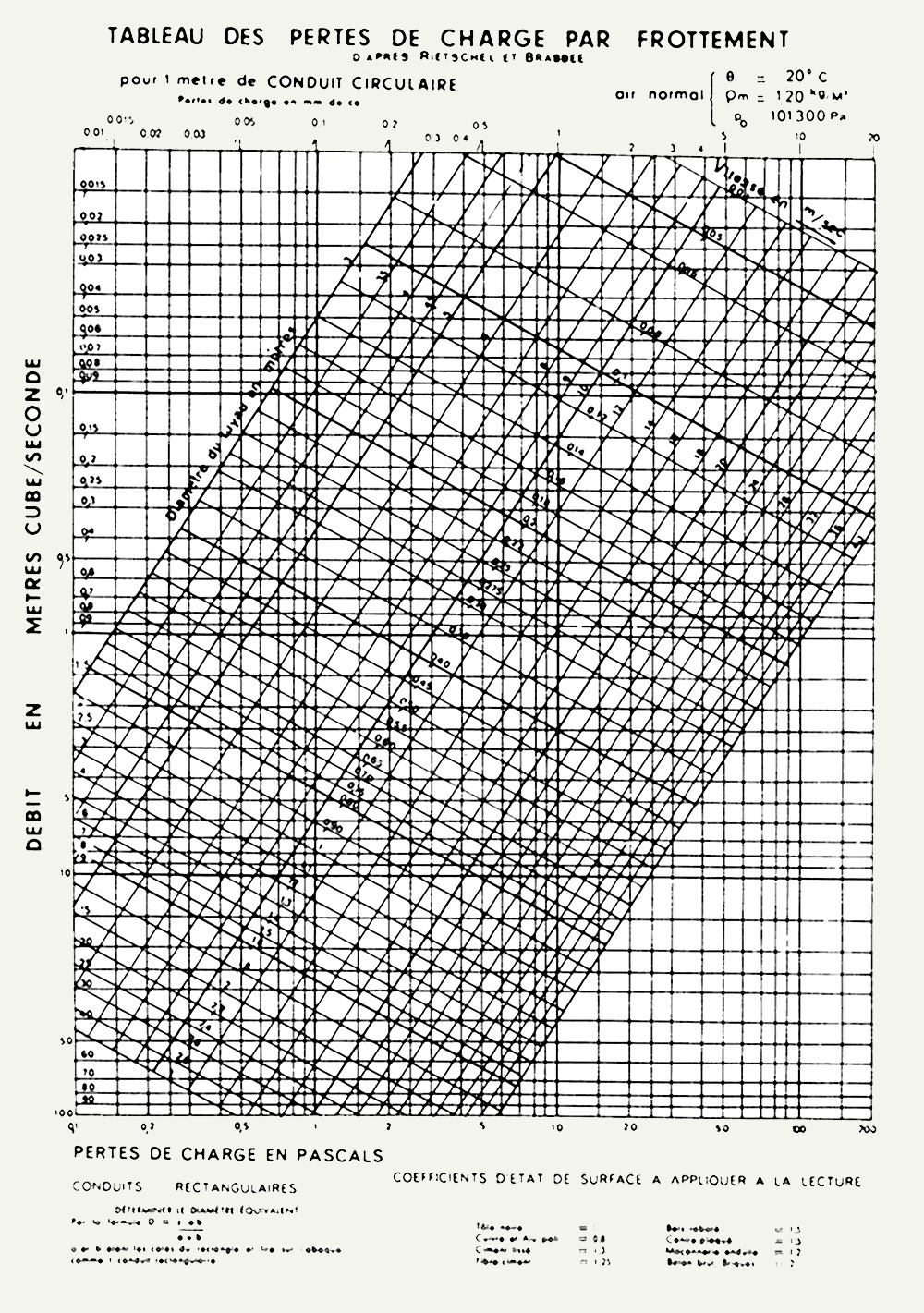
Mais en règle générale on se sert d'abaques du type de celui présenté Figure 9 (Tableau de pertes de charge par frottement d'après RIETSCHEL et BRABEE).
Il en est de même pour le calcul des pertes de charge particulières comme les coudes, les
culottes de dérivation, les étranglements ou élargissements ou:
![]()
K coefficient de singularité donné dans la bibliographie et certains abaques (voir ci dessous)
- Figure 8 :
Exemples (pour mémoire) de valeurs du coefficient de pertes de charge singulières k
pour des éléments non aérodynamiques
Figure 9 :
Pertes de charge par frottement dans des gaines circulaires en tôles noire lisses
Note : La notion de hauteur manométrique en mm de Colonne d'Eau (mm CE) est intéressante à retenir. En effet un technicien dépourvu de manomètre pourra toujours confectionner ce dernier en utisant une planchette retenant un simple tuyau plastique transparent placé en "U" avec un peu d'eau.